研究

情報流体力学

乱流中のエネルギカスケードと小スケールの普遍性

字の示すとおり時空間的に「乱」れた「流」れである乱流は，われわれの身のまわりにありふれた現象でありながら予測や制御がきわめて困難な「古典力学に残された最後の難問」と言われています． その例として，天気予報が100%当たるわけではないことや飛行機の翼周りの流れを抵抗の少ない層流（=整った流れ）で維持できないことなどが挙げられます． 乱流はさまざまなスケールの渦の複雑な相互作用として解釈されることが多く，Richardsonの「渦の詩」では時々刻々その形を変化させる積雲が：

[…] big whirls have little whirls that feed on their velocity, and little whirls have lesser whirls and so on to viscosity […].

（訳）大きな渦は小さな渦を従えそれらに速度を供給し，小さな渦はさらに小さな渦を従えることを繰り返して粘性に至る．

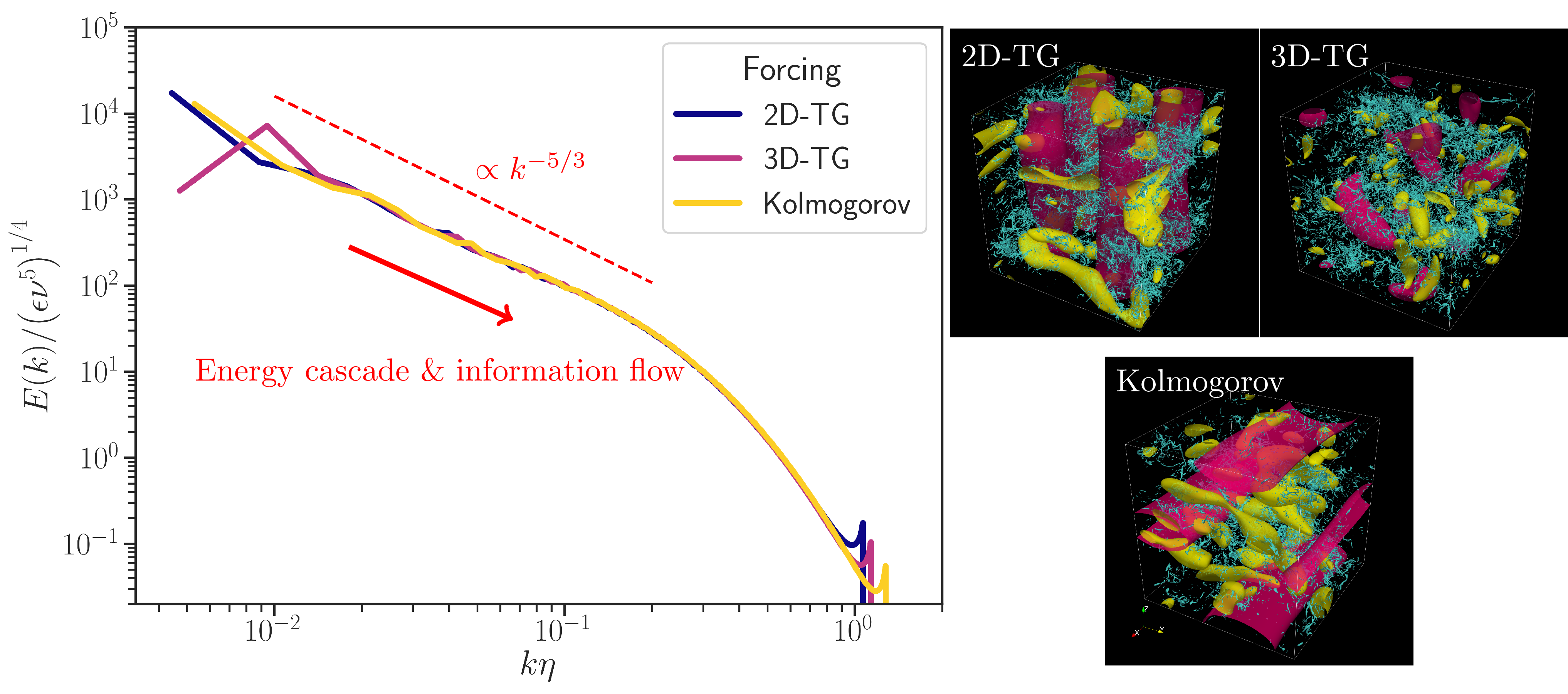
と描写されています． この大スケールの渦へ注入されたエネルギが小スケールの渦へ段階的に伝わって（=カスケードして）いき，粘性が支配するスケールから熱として散逸する，という乱流のエネルギカスケード描像は，今日では広く受け入れられています．

この描像と並んで重要なのが乱流の小スケールにおける統計的な普遍性です． これは，流れのマクロな特徴が異なっていても，例えば大気の運動でも飛行機の翼周りの流れでも，乱流中の小スケール（小さな渦）は普遍的な統計を示す，という性質です． 確率論でも有名なKolmogorovが1941年の論文群で理論的に提案して以来，この普遍則はさまざまな流れの実験，数値計算，そして理論解析で成立することが確かめられ，乱流研究のパラダイムとなっています．

乱流の小スケール統計普遍性の起源はエネルギカスケード描像にあるとされており，エネルギが大から小スケールへ伝わる過程で流れがそのマクロな特徴を「忘れて」しまうために小スケールが普遍的な統計を示す，という説明がしばしばなされます． 例えると，自身より小さいスケールへ段階的にエネルギを伝えるエネルギカスケード描像はあたかも「乱流の大スケールと小スケールの間をたくさんの人（=異なるスケールの渦）でつないだ糸電話」のように捉えることができ，しばしば失敗する伝言ゲームと同じように乱流中の大スケールの渦がもつ情報も小スケールでは失われてしまうというのです．

情報理論⨉乱流

しかし，上記の説明では乱流の大スケールがもつ情報が小スケールにたどり着くまでにどのように失われてしまうのかが分かりません． また，エネルギカスケード描像は大スケールの渦が小スケールの渦をつくる（エネルギを与える）と言っているのですから，そこには因果関係（=情報の輸送）が存在するはずで，大スケールの情報が小スケールですべて失われるというわけでもなさそうです． これはちょうど，伝言ゲームの結果が完全にランダムな文字列にはなりそうもないことと対応しています．

このような疑問を出発点に，我々は「情報」の視点から新しい乱流描像を構築することにとりくんでいます． ここで情報とは，Shannonがノイズのある経路での通信効率を調べた研究で信号の不確かさを定量化するために導入した量で，その指標が情報エントロピです． 大きな情報エントロピは次に生じる事象の不確定性が高い（=観測したときの驚きが大きい）ことを，反対に小さなときは次に生じる事象がほぼ確定している（=観測しても驚きがない）ことを意味します． 今日，この情報理論はいわゆるIT分野のみならず物理学のさまざまな分野へさかんに応用されています（参考：CRDS: 情報・物理・数理の共創　～非平衡ダイナミクスの理解が見せる新たな景色～）．

情報の視点から乱流を捉え直すと，さまざまな問題を新しく定式化できます． この文章で議論したのは「発達した乱流の小スケールは大スケールの情報をどの程度，どのように忘れている（覚えている）のか？」という乱流理論の基礎に関わるものでしたが，他にも層流-乱流遷移の確率的な記述やカオス理論による乱流の特徴づけ，乱流モデルへの応用など，きわめて多彩な研究課題を考えることができます． このように情報の視点から捉え直す流体力学，すなわち「情報流体力学」は，これまでの乱流研究のパラダイムに大きな変化をもたらしうる可能性をもっています．

情報熱力学⨉乱流

情報熱力学とは情報を定式化に取り込んだミクロスケールの熱力学のことで，近年の非平衡統計力学の活発な進展に重要な寄与を果たしています． 中でも重要な成果として，系を構成する分子の運動を測定・制御して熱力学的エントロピを減らす（=熱力学第二法則に反する）能力をもつMaxwellのデーモンのパラドックスを，デーモンの情報処理を含む系に拡張して解決したことが挙げられます． ただ，流体力学の講義のはじめに習う「流体力学が対象とするのは原子や分子よりも十分大きくミクロな熱ゆらぎが無視できるスケールにおける流れである」という前提をふまえると，情報熱力学と乱流の組み合わせは対象とするスケールが離れすぎていて意味をなさないように思えます． しかし近年，ミクロな熱ゆらぎが影響を及ぼすスケールと乱流の最小スケールはそれほど離れておらず，最小スケール渦のふるまいにはミクロな熱ゆらぎが本質的な寄与を果たす，と主張する論文がいくつか報告されています．

我々はこのような先行研究をふまえ，情報熱力学の立場から乱流を調べています． 直近では，乱流中のエネルギカスケードに伴って生じる大から小スケールへの情報輸送が存在することを情報熱力学第二法則から証明し，数値的にも検証しました． この研究は，マクロな熱力学と流体力学を組み合わせた熱流体力学―天気予報やエアコンの設計に応用される学問―とはまったく異なるアプローチをとっています． 我々は，情報熱力学で明らかになった情報の流れに関する普遍則を軸にして「情報流体力学」を展開していきたいと考えています．